#2032. 「IOI 2023」足球场

Debrecen 市有一片正方形的森林名叫 Nagyerdő，可以看作是 的方格。方格的行由北向南从 到 编号，列由西向东从 到 编号。方格中第 行第 列的格子被称为单元格 。

森林里的每个单元格要么是空的，要么是有树的。森林里至少有一个空单元格。

DVSC 是这个城市最著名的体育俱乐部，目前正计划在森林里修建一座新的足球场。大小为 的球场（这里 ）是 个互不相同的空单元格 的集合。形式化地说，这意味着：

• 对于从 到 （包含两端）的每个 ，单元格 是空的；
• 对于满足 的每组 和 ， 和 二者中至少有一个成立。

踢球时足球在球场的单元格之间传递。直传是以下两种动作之一：

• 球场包含第 行中单元格 和 之间的全部单元格，球从单元格 传递到单元格 （）。包含关系的形式化定义为：
  • 若 ，则球场应包含满足 的每个单元格 ；
  • 若 ，则球场应包含满足 的每个单元格 。
• 球场包含第 列中单元格 和 之间的全部单元格，球从单元格 传递到单元格 （）。包含关系的形式化定义为：
  • 若 ，则球场应包含满足 的每个单元格 ；
  • 若 ，则球场应包含满足 的每个单元格 。

如果可以通过至多 次直传将球从球场的任意单元格传递到另外的任意单元格，那么称这样的球场是规则的。注意，任何大小为 的球场都是规则的。

例如，考虑一片大小为 的森林，其中单元格 和 有树，其余单元格均为空。 下图显示了三个可能的球场。有树的单元格用深色表示，组成球场的单元格划有斜线。

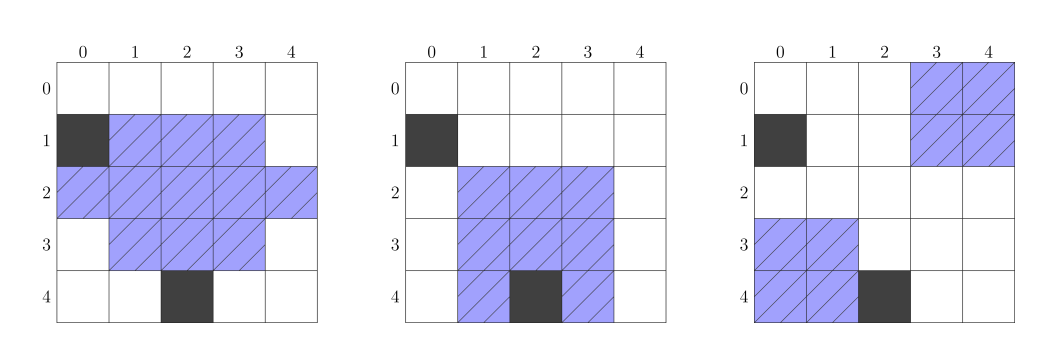
左边的球场是规则的。然而，中间的球场不是规则的，原因是把球从单元格 传递到单元格 至少需要 次直传。右边的球场也不是规则的，原因是无法通过直传将球从单元格 传递到单元格 。

体育俱乐部希望建造尽可能大的规则球场。 你的任务是找出最大的 值，使得森林里可以建造大小为 的规则球场。

你需要在程序开始引入库 soccer.h。

你要实现以下函数：

int biggest_stadium(int N, int[][] F)

• ：森林的大小。
• ：一个长度为 的数组，每个元素都是长度为 的数组，用于描述森林里的单元格。对于每组满足 且 的 和 ， 表示单元格 是空的， 表示该单元格是有树的。
• 这个函数应该返回森林里可以建造的规则球场的最大大小。
• 对于每个测试用例，这个函数恰好被调用一次。

考虑以下调用：

biggest_stadium(5, [[0, 0, 0, 0, 0],  
                    [1, 0, 0, 0, 0], 
                    [0, 0, 0, 0, 0], 
                    [0, 0, 0, 0, 0], 
                    [0, 0, 1, 0, 0]])

这个例子描述的森林显示在下图的左边，一个大小为 的规则球场显示在下图的右边：

由于不存在大小为 或更大的规则球场，函数应该返回 。

• （对满足 且 的所有 和 ）
• 森林里至少存在一个空单元格。也就是说，对于某组满足 且 的 和 ，有 。

1. （6 分）至多只有一个单元格有树。
2. （8 分）
3. （22 分）
4. （18 分）
5. （16 分）
6. （30 分）没有额外的约束条件。

在每个子任务中，如果你的程序能够正确判定全部空单元格组成的集合能否构成一个规则球场，那么你将在该子任务获得 25% 的部分分。

更准确地讲，对于所有空单元格组成的集合是一个规则球场的测试用例，你的解答的得分情况如下：

• 如果返回正确答案（也就是所有空单元格的数量），则得满分；
• 否则得 0 分。

对于所有空单元格组成的集合不是一个规则球场的测试用例，你的解答的得分情况如下：

• 如果返回正确答案，则得满分；
• 如果返回所有空单元格的数量，则得 0 分；
• 如果返回其他值，则得 25% 的分数。

每个子任务的得分是这个子任务中所有测试用例得分的最低值。

评测程序示例按以下格式读取输入：

• 第 行：
• 第 行（）：

评测程序示例按以下格式打印你的答案：

• 第 行：函数 biggest_stadium 的返回值