Vétyem Woods 是一片著名的缤纷多彩的森林。其中最老最高的一棵山毛榉树叫 Ős Vezér。
树 Ős Vezér 可以被建模成 个结点和 条边的集合。结点的编号为从 到 ,边的编号为从 到 。每条边均连接树上两个不同的结点。具体地说,边 ()从结点 连接到结点 ,这里 。结点 被称为是结点 的父结点,而结点 被称为是结点 的一个子结点。
每条边都有某种颜色。一共有 种可能的颜色,编号为从 到 。边 的颜色为 。不同的边可能有相同的颜色。
注意,在上面的定义中, 的情形并不对应树上的边。方便起见,我们令 和 。
例如,假定 Ős Vezér 有 个结点和 种可能的颜色,以及 条边。边的描述为 ,边的颜色为 。这棵树如下图所示:
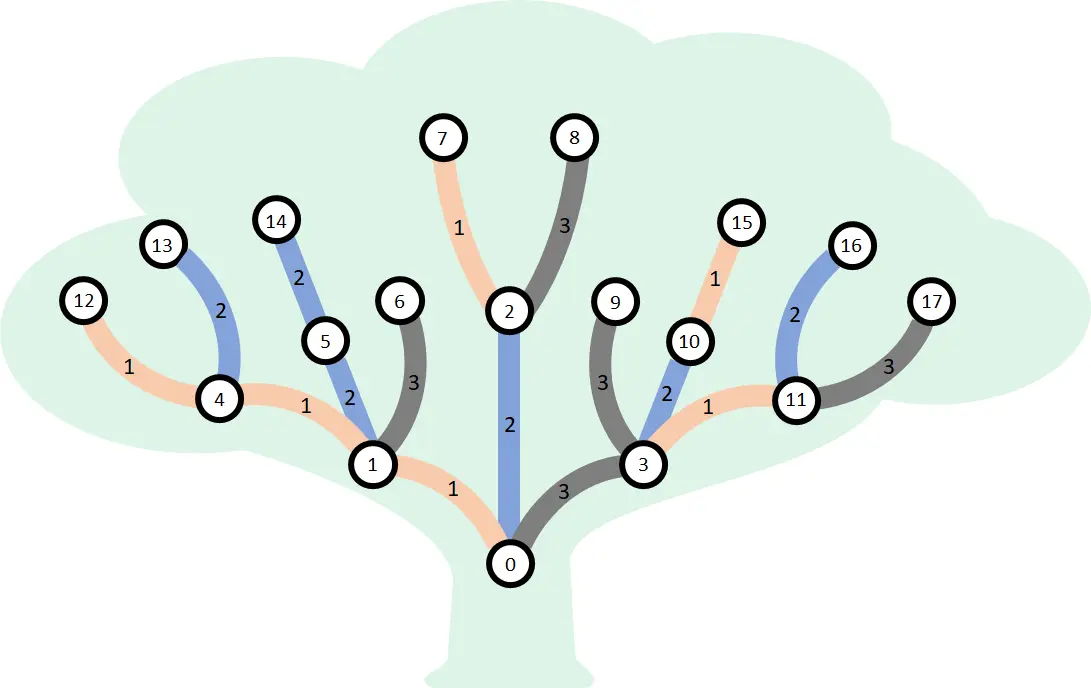
Árpád 是一位才华横溢的护林人,他喜欢研究树上被称为子树的部分。
对所有满足 的 ,结点 的子树是一个满足以下性质的结点集合 :
- 结点 属于 。
- 如果某个结点 属于 ,则 的所有子结点都属于。
- 除了上述情况以外,其他结点都不属于 。
集合 的大小记作 。
Árpád 最近发现了一个复杂但有趣的子树性质。Árpád 的发现需要用到大量的纸和笔做演算,他认为你需要做同样的事情才能完成理解。他还会给你几个例子,让你能够对它们做详细的分析。
假设我们有某个给定的 ,以及子树 中结点的某个置换 。
对于所有满足 的 ,令 为颜色 在长为 的颜色序列 中的出现次数。
(注意, 必定为 ,原因是其定义中要考察的颜色序列是空的。)
置换 被称为是一个绝妙置换,当且仅当以下性质成立:
对于所有满足 的 ,子树 是一棵绝妙子树,当且仅当 中结点存在某个绝妙置换。注意,根据定义,仅包含单独一个结点的子树都是绝妙的。
考虑上面给出的树的例子。可以看到,子树 和 不是绝妙的。子树 是绝妙的,因为它仅包含一个结点。接下来,我们将要说明子树 也是绝妙的。
考虑一个由不同整数构成的序列 。这个序列是 中结点的一个置换。下图给出了这个置换。序列中每个结点旁边的数字,是该结点在置换中的索引。
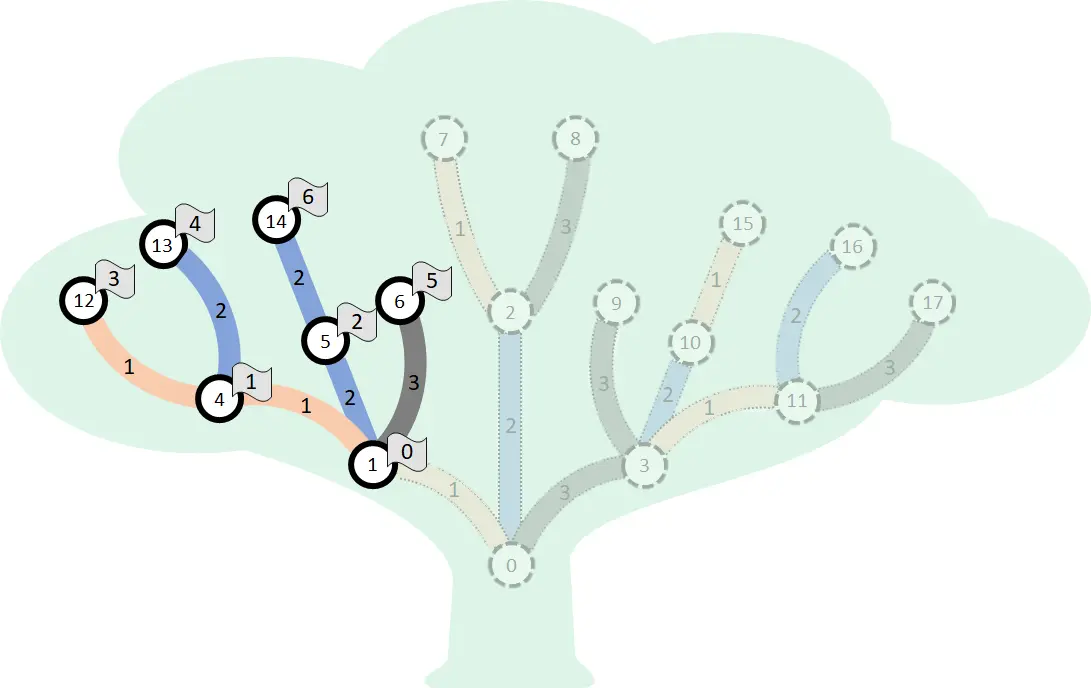
我们将要验证,这是一个绝妙置换。
- 。
- ,原因是 在序列 中出现了 次。
- 相应地, 的父结点是 。也就是说, 的父结点是 。(形式化地,。)
- ,原因是 在序列 中出现了 次。
- 相应地, 的父结点是 。也就是说, 的父结点是 。
- ,原因是 在序列 中出现了 次。
- 相应地, 的父结点是 。也就是说, 的父结点是 。
- ,原因是 在序列 中出现了 次。
- 相应地, 的父结点是 。也就是说, 的父结点是 4。
- ,原因是 在序列 中出现了 次。
- 相应地, 的父结点是 。也就是说, 的父结点是 。
- ,原因是 在序列 中出现了 次。
- 相应地, 的父结点是 。也就是说, 的父结点是 。
由于我们能为 中的结点找到一个绝妙置换,子树 因此是一棵绝妙子树。
你的任务是,帮助 Árpád 确定 Ős Vezér 的每棵子树是否是绝妙的。